作為一種α+β相耐熱鈦合金,鈦合金TC11具有高強度、超強耐腐蝕性、優(yōu)異的抗蠕變性和較好的熱穩(wěn)定性,被廣泛應用于航空發(fā)動機渦輪盤、葉片等重要構件。在鈦合金切削過程中切削溫度較高、切削力較大,刀具容易磨損,加工效率整體較低,加工表面容易產(chǎn)生表面微裂紋、加工硬化等現(xiàn)象。國內外學者對鈦合金加工進行了大量的研究:岳彩旭、張統(tǒng)等利用ABAQUS軟件建立了平底銑刀銑削鈦合金TC4的C形薄壁零件仿真模型,結果表明有限元模型可以預測銑削力;劉昂馳等對鈦合金TC4進行了順銑和逆銑加工研究,結果表明逆銑銑削力大于順銑銑削力;從政、楊振朝等分別針對鈦合金TC11進行車削仿真和高速銑削試驗,得出工藝參數(shù)對切削力的影響規(guī)律。
上述研究主要是針對用平底銑刀銑削鈦合金的情況,但渦輪盤、葉片等是由復雜自由曲面構成的零件,多采用球頭刀配合小切削深度來加工側壁,加工效率低。相比于球頭刀,錐度球頭刀的曲面部分由一個大曲率半徑圓弧構成7,能夠增大刀具整體的剛性,可承受較大的切削深度,被廣泛應用于航空薄壁零件的高效加工。由于錐度球頭刀可以承受較大的切削深度,因此編程時可以縮短
刀具路徑,提高生產(chǎn)效率。
隨著五軸加工技術和CAM的發(fā)展,錐度球頭刀被廣泛應用于復雜曲面?zhèn)缺诘母呔群透咝始庸ぁ1疚牡难芯勘尘盀楹娇崭叨酥圃臁皩>匦隆碑a(chǎn)業(yè)學院中西安亞太菁英智能裝備有限公司生產(chǎn)項目。為解決薄壁零件加工變形問題,有必要對錐度球頭刀銑削鈦合金TC11的切削力進行研究,為實現(xiàn)薄壁零件高質、高效銑削加工提供理論支撐。
1、試驗方案
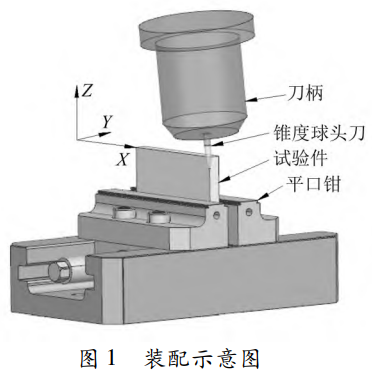
切削試驗材料為鈦合金TC11,試驗件尺寸為100mmx10mmx50mm,試驗件采用平口鉗夾持的方法固定在機床工作臺上,試驗件長度方向沿X軸方向,如圖1所示。刀具采用整體硬質合金6 mm錐度球頭刀,刀齒個數(shù)為4。采用刀具側刃進行銑削加工,切削寬度為0.2mm。
切削力是表征切削過程穩(wěn)定性的重要物理量之一,它的大小會影響表面完整性、薄壁零件變形程度和刀具耐用度。為了研究切削速度[v。]、切削深度[a]和每齒進給量[f]3個工藝參數(shù)對主切削力[F1]的影響,采用田口法進行三因素三水平的正交試驗分析,各參數(shù)所對應水平見表1。
表1試驗因素及水平
| 序號 | 參數(shù) | 水平 1 | 水平2 | 水平 3 |
| A | 切削速度 v c /[m/min] | 30 | 40 | 50 |
| B | 切削深度 a p /mm | 7 | 8 | 9 |
| C | 每齒進給量 f z /[mm/z] | 0.02 | 0.04 | 0.06 |
2、切削仿真分析方法
在建立的切削仿真三維模型中,需要對材料的本構模型、斷裂準則、比熱、密度、泊松比等進行參數(shù)設定。切削仿真過程涉及材料的彈性、塑性硬化和斷裂過程間。塑性屈服與應變硬化采用 John-son-Cook塑性模型,因為其擁有能夠很好地描述金屬在大應變、高應變率和高溫下的本構方程,見公式[1]。
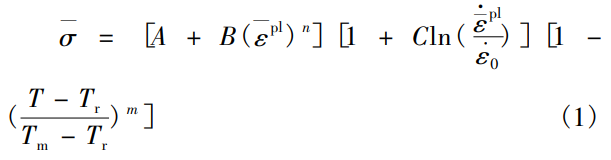
式中: σ為材料的流動應力, MPa; A為屈服應力強度, MPa; B為應力強化常數(shù); ε pl為等效塑性應變; n為應變強化指數(shù); C為應變率強化參數(shù); ε ˙ pl為等效塑性應變率; ε ˙ 0 為參考應變率,取 1.0 s ?1; T為樣品的環(huán)境溫度,℃;T為室溫,℃;T為材料的熔點,℃;m為溫度應變率靈敏度。表2為鈦合金TC11材料 Johnson-Cook塑性參數(shù)。
表2 TC11材料 Johnson-Cook塑性參數(shù)
| A/MPa | B/MPa | C | m | n | Tr/℃ | Tm/℃ |
| 1309 | 258 | 0.44 | 0.99 | 0.44 | 20 | 1660 |
材料的失效準則采用 Johnson-Cook損傷模型,其中失效應變 ε D pl 由公式[2]計算,TC11的Johnson-Cook失效參數(shù)見表3。
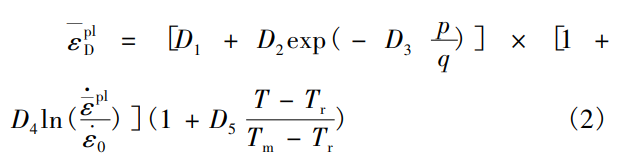
式中: D 1 ~ D 5 為失效參數(shù), p為靜水應力, q為米塞斯應力。
表 3 TC11的 Johnson- Cook失效參數(shù)
| D 1 | D 2 | D 3 | D 4 | D 5 |
| -0.09 | 0.27 | 0.48 | 0.01 | 3.87 |
結合試驗工藝參數(shù)完成刀具和工件的裝配。分別采用 C3D10和 C3D8R單元對刀具和工件進行網(wǎng)格劃分,刀具網(wǎng)格尺寸應大于工件網(wǎng)格尺寸。將刀具設置為剛體和主動面,工件設置為從動面,刀具和工件之間的相互作用模式為通用接觸,包括面-面接觸和工件的自接觸。最后對工件施加固定約束,對刀具施加移動速度和旋轉速度,完成銑削加工模擬仿真。
3、試驗結果分析
3.1影響規(guī)律分析
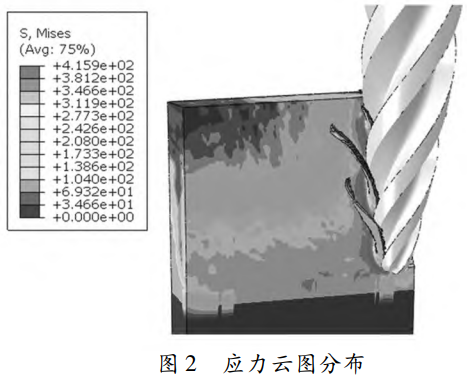
切削參數(shù)為 vc=30m/min、fz=0.06mm/z、 ap=9mm時,銑削加工應力云圖如圖 2所示,可以看出, Mises應力最大值出現(xiàn)在刀具和工件的接觸點。這是由于在該變形區(qū)切削層受到刀具的剪切與擠壓作用,接觸面材料的應力值達到材料的斷裂極限,開始出現(xiàn)切屑分離 [13]。仿真產(chǎn)生的切屑形狀為帶狀結構,并且出現(xiàn)了一定的卷曲,切屑貼近刀具的螺旋槽發(fā)生卷曲。切削仿真所產(chǎn)生的切屑形態(tài)與生產(chǎn)加工鈦合金產(chǎn)生的切屑形態(tài)[如圖 3所示)近似。
結合圖1可知,X軸方向對應于刀具的進給方向,Y軸方向表示刀具的徑向方向,Z軸方向指的是銑削刀具的軸向方向。刀具徑向切削力最大,是
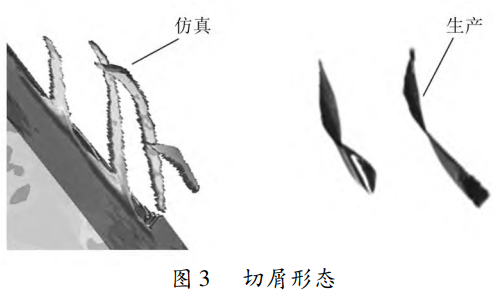
引起薄壁工件變形的重要原因,因此本文將重點研究刀具的徑向切削力。切削參數(shù)為vc=30m/min、fz=0.06mm/z、 ap=9mm時,切削力隨時間的變化如圖4所示。隨著時間的增加,切削力呈周期性變化。在一個切削周期內,隨著刀齒的切入、切出,切削力先增大后減小,切削力最大值時刻切削面積最大。
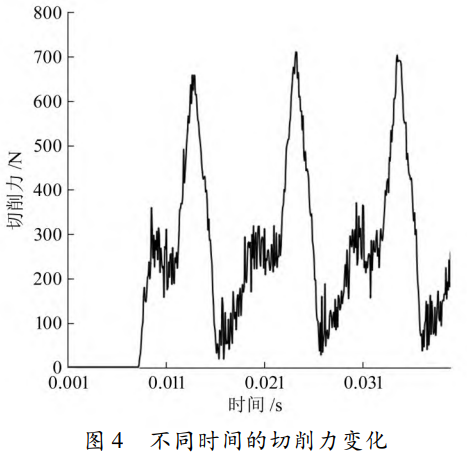
依次按照三因素三水平正交試驗表的順序完成切削仿真,獲得的切削力結果見表 4。
表4正交試驗設計及結果
| 序號 | vc/[m/min] | ap /mm | fz/[mm/z] | 切削力F/N |
| 1 | 30 | 7 | 0.02 | 330.04 |
| 2 | 30 | 8 | 0.04 | 469.11 |
| 3 | 30 | 9 | 0.06 | 702.08 |
| 4 | 40 | 7 | 0.04 | 450.21 |
| 5 | 40 | 8 | 0.06 | 588.18 |
| 6 | 40 | 9 | 0.02 | 432.32 |
| 7 | 50 | 7 | 0.06 | 368.44 |
| 8 | 50 |
| 0.02 | 330.16 |
| 9 | 50 | 9 | 0.04 | 596.63 |
為了獲得工藝參數(shù)對切削力的影響規(guī)律,采用田口法進行分析。根據(jù)表 4中的數(shù)據(jù)結果,分別計算出各因素在每個水平條件下的切削力平均值和極差,最終得到均值響應表[表5]。極差的大小反映了每個試驗因素對切削力結果影響的強弱,對切削力影響最大的工藝因子是切削深度,其次是每齒進給量,切削速度最小。
表5均值響應表
| vc/[m/min] | ap/mm | fz/[mm/z] |
| 1 | 500.4 | 382.9 | 364.2 |
| 水平 2 | 490.2 | 462.5 | 505.3 |
| 3 | 431.7 | 577.0 | 552.9 |
| 極差 | 68.7 | 194.1 | 188.7 |
| 排序 | 3 | 1 | 2 |
3.2建立切削力預測模型
采用多元線性回歸法對表 4所示的測試數(shù)據(jù)進行擬合,切削速度 [v c ]、切削深度 [a p ]和每齒進給量 [f z ]作為自變量,切削力 [F 1 ]作為因變量,建立錐度球頭刀銑削鈦合金TC11的切削力預測模型,如式[3]所示。
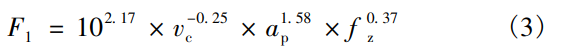
對預測模型進行方差分析,是驗證其準確性和可用性的方法之一。式(4)所示預測模型的方差檢驗見表 6。由表可知,切削力預測模型中回歸項的 P小于 0.05,即預測模型顯著,可以實現(xiàn)對切削力的準確預測。
表6切削力預測模型的方差檢驗
| 來源 | 自由度 | 平方和 | 均方 | F | P |
| 模型 | 3 | 0.096 6 | 0.032 2 | 12.43 | 0.009 |
| 誤差 | 5 | 0.0129 | 0.0026 |
|
|
| 合計 | 8 | 0.109 |
|
|
|
模型預測結果和切削力試驗結果的對比如圖5所示。可以看出,預測模型對 9組試驗結果變化趨勢的預測是準確的,其中第 7組參數(shù)組合的切削力誤差最大為 15.36%;第 1組參數(shù)組合的切削力誤差最小僅為2.55%;9組試驗的平均切削力誤差為7.45%。
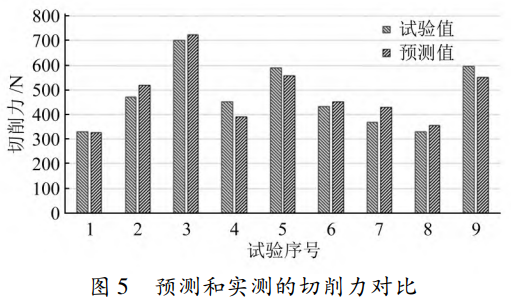
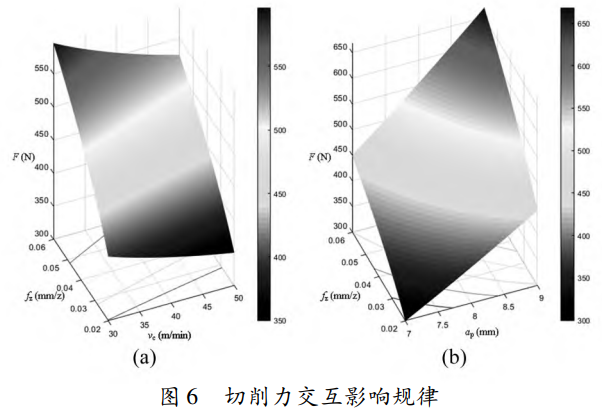
圖6[a]為當a_{p}=8mm時,切削速度和進給量對切削力的交互影響規(guī)律。可以觀察到在30~50 m/min的切削速度范圍內,切削力表現(xiàn)出遞減趨勢。這一現(xiàn)象可以解釋為增加切削速度導致被加工工件材料的塑性變形減小,同時引發(fā)了剪切角增大,從而導致切削力降低。提升切削速度還會引發(fā)更多切削熱量的產(chǎn)生,進一步強化材料的熱軟化效應。圖6[b]為當v。=40m/min時,切削深度和進給量對切削力的交互影響規(guī)律。隨著切削深度和進給量的增大,切削力也隨之增大。產(chǎn)生這種現(xiàn)象的主要原因是,隨著切削深度的增大,錐度球刀與工件接觸的圓弧長度增加,使得切削面積增大,導致變形力增大,摩擦力也增大。隨著進給量的增大,單位時間內參與切削的材料體積增大,刀具與材料和切屑之間的摩擦增加,切削力不斷增大。
4、結束語
本文給出的分析銑削力變化規(guī)律的方法和預測模型建模方法通用性較強,為錐度球頭刀切削金屬材料的切削力預測提供了一種思路。但是,實際
銑削加工過程中需要考慮的因素很多,本文仿真所用為實際工件的簡化模型,還需和企業(yè)聯(lián)合開展相關試驗,以進一步優(yōu)化模型。
參考文獻
[1] BANERJEE D, WILLIAMS J C. Perspectives on titanium science and technology[J]. Acta Materialia,2013,61[3]:844-879.
[2]岳彩旭,胡德生,劉獻禮,等.基于有限元仿真的鈦合金薄壁件銑削參數(shù)優(yōu)化.工具技術,2021,55[11]:53-60.
[3]張統(tǒng).鈦合金薄壁件銑削加工變形預測與參數(shù)優(yōu)化研究[D].哈爾濱:哈爾濱理工大學,2020.
[4]劉昂馳,寧立偉,梁桂強,等.鈦合金順銑和逆銑的有限元仿真對比分析.工具技術,2022,56[1]:32-37.
[5]從政,曹巖,賀志昊,等.TC11鈦合金力熱耦合仿真分析及雙目標參數(shù)優(yōu)化[J].制造技術與機床,2022[1]:119-123.
[6]楊振朝,林允博,劉三娃,等.基于 Box-Behnken設計的高速銑削TC11鈦合金切削力預測模型研究[J].航空精密制造技術,2018,54[4]:14-18.
[7] URBIKAIN G,LACALLE L DE, NORBERTO L. Bridging the gap between student instruction and advanced research: educational software tool for manufacturing learning[J]. Computer Applica-tions in Engineering Education,2021,29[1]:274-286.
[8] PELAYO G U. Modelling of static and dynamic milling forces in inclined operations with circle-segment end Mills[J].Precision Engineering,2019,56:123-135.
[9]王威振,姜增輝,陳興寬,等.切削參數(shù)對高速銑削Stellite6合金切削力的影響[J].兵器材料科學與工程,2023,46[3]:129-133.
[10] AYDIN M. Numerical study of chip formation and cutting force in high-speed machining of Ti-6Al-4V bases on finite element modeling with ductile fracture criterion[J]. International Journal of Material Forming,2021,14[5]:1005-1018.
[11]從政.TC11鈦合金航空盤類零件車削工藝優(yōu)化研究[D].西安:西安工業(yè)大學,2022.
[12]李偉,周蘭,王林軍,等.基于材料損傷演化的鈦合金螺旋銑孔切削力仿真模型.蘭州理工大學學報,2023,49[2]:56-64.
[13]王明海,李世永,王京剛,等.航空鈦合金Ti6Al4V的三維銑削加工有限元仿真[J].機械科學與技術,2014,33[7]:1036-1039.
(注,原文標題:錐度球頭刀銑削鈦合金TC11切削力研究)
無相關信息